What is Euler Angle A, B, C?

Euler Angle is a way to express the angles of X, Y and Z axes, which are perpendicular among themselves in the object direction. A, B and C refer to the sequential rotation angles. Each robot manufacturer defines this A, B and C rotation order differently, such as Rz-Ry-Rx or Rx-Ry-Rz.

Doosan Robotics uses Rz-Ry-Rz. Here, Rz means the rotation in Z-axis, and Ry means the rotation in Y-axis. Rz can be expressed as angle A, Ry as angle B, and Rz as angle C to indicate the current rotating direction of an object. Note that once rotation is made in Z-axis direction from the coordinates, rotations will be made based on new coordinates.

This can be visualized with steps 1 to 4.

1. Assume there are coordinates (X, Y, Z).
   

   

   
   
   

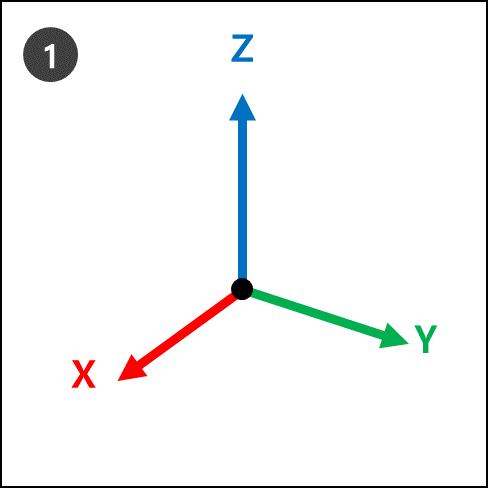
2. Rz: Rotate by A degrees from the Z-axis.
   

   

   
   
   

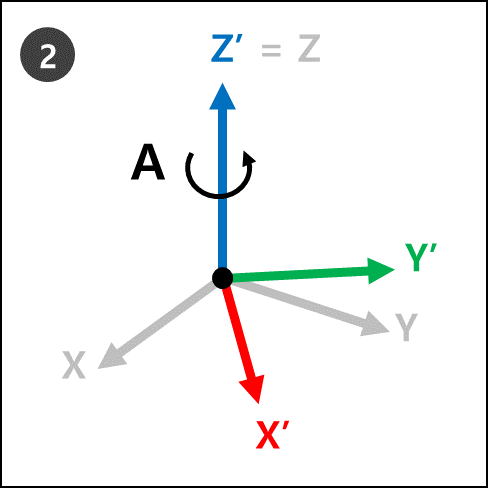
3. Ry : Rotate by B degrees from the new Y-axis (Y’) of the new coordinates (X’, Y’, Z’) in step 2.
   

   

   
   
   

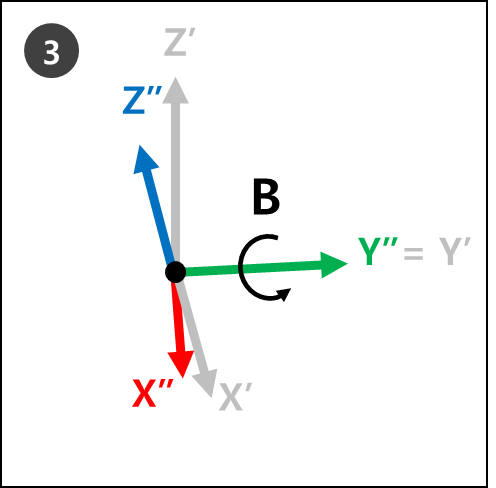
4. Rz : Rotate by B degrees from the new Z-axis (Z’’) of the new coordinates (X’’, Y’’, Z’’) in step 3.
   

   

   
   

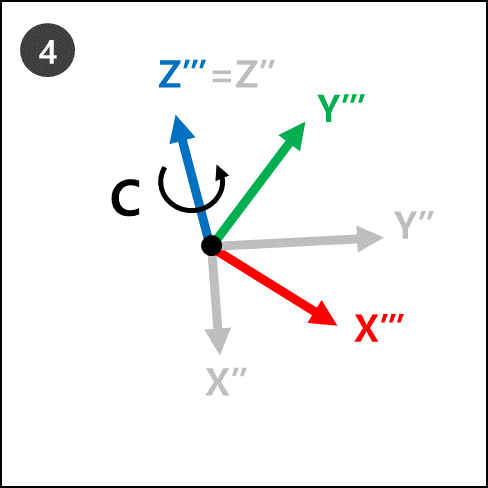
5. The new coordinates (Z’’’, Y’’’, X’’’ of step 4 refers to the current robot rotation when Euler Angles A, B and C are applied.

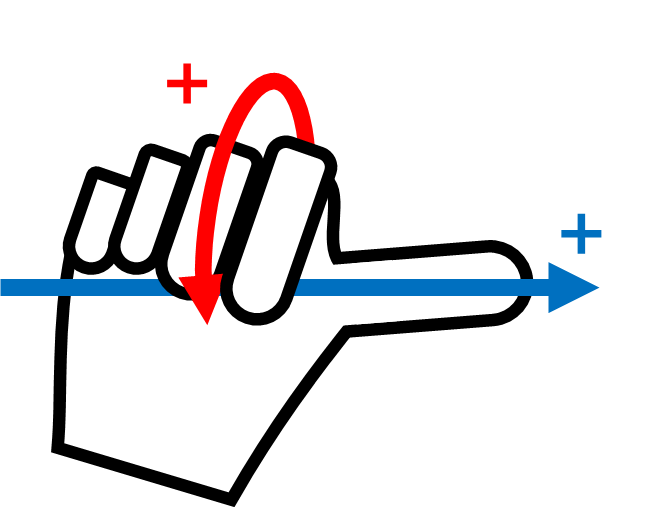
This can be easily visualized with one’s right hand. Make the following pose with your right hand. This is called the Right-Hand Rule, and making the thumb (X-axis), index finger (Y-axis) and middle finger (Z-axis) to be perpendicular to each other will create coordinates consisting of X, Y and Z axes.

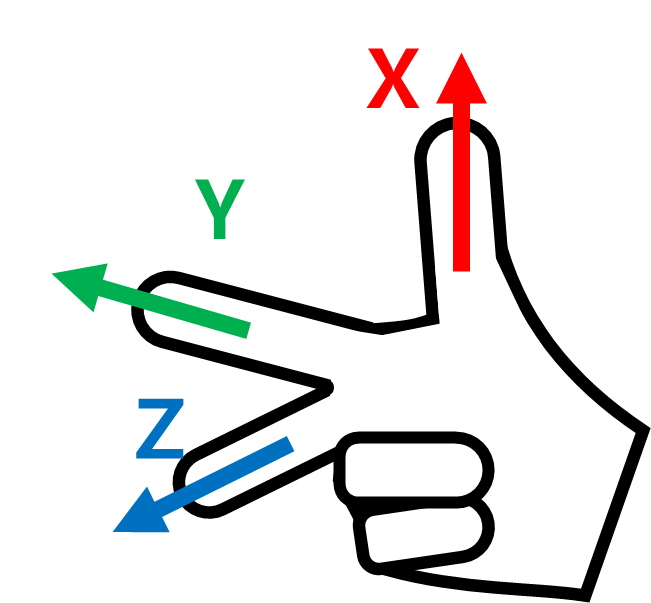
Then make the Right-Hand Rule Cartesian pose and make rotations Rz, Ry and Rz in sequential order.

1. Rz: Rotate the middle finger (Z-axis) by A degrees. 

2. Ry: Rotate the index finger (Y-axis) by B degrees.

3. Rz: Rotate the middle finger (Z-axis) by C degrees.

Note

The + rotating direction of A, B and C is the direction of four fingers except the thumb, when the thumb is pointing at the + direction and the four fingers are clenched. This is called the Law of Clockwise Screw.